Deriváty vyššího řádu

Naposledy aktualizováno 31. července 2021

deriváty vyššího řádu mohou zachytit informace o funkci, kterou deriváty prvního řádu samy o sobě nemohou zachytit.

deriváty prvního řádu mohou zachytit důležité informace, jako je rychlost změny,ale samy o sobě nemohou rozlišovat mezi lokálními minimy nebo maximy, kde rychlost změny je nulová pro oba. Několik optimalizačních algoritmů řeší toto omezení využitím použití derivátů vyššího řádu, například v Newtonově metodě, kde se deriváty druhého řádu používají k dosažení lokálního minima optimalizační funkce.

v tomto tutoriálu zjistíte, jak vypočítat jednorozměrné a vícerozměrné deriváty vyššího řádu.

po dokončení tohoto tutoriálu budete vědět:

• Jak vypočítat deriváty vyššího řádu jednorozměrných funkcí.
• jak vypočítat deriváty vyššího řádu vícerozměrných funkcí.
• jak lze deriváty druhého řádu využít ve strojovém učení pomocí optimalizačních algoritmů druhého řádu.

začněme.

přehled tutoriálu

tento tutoriál je rozdělen do tří částí; jsou:

• deriváty vyššího řádu jednorozměrných funkcí
• deriváty vyššího řádu vícerozměrných funkcí
• aplikace ve strojovém učení

deriváty vyššího řádu jednorozměrných funkcí

kromě derivátů prvního řádu, které jsme viděli, nám mohou poskytnout důležité informace o funkci, jako je její okamžitá rychlost změny, deriváty vyššího řádu mohou být také stejně důležité.užitečné. Například druhá derivace může měřit zrychlení pohybujícího se objektu nebo může pomoci optimalizačnímu algoritmu rozlišovat mezi lokálním maximem a lokálním minimem.

výpočet derivátů jednorozměrných funkcí vyššího řádu (druhé, třetí nebo vyšší) není tak obtížný.

druhá derivace funkce je pouze derivací její první derivace. Třetí derivát je derivát druhého derivátu, čtvrtý derivát je derivát třetího a tak dále.

– Strana 147, kalkul pro figuríny, 2016.

proto výpočet derivátů vyššího řádu jednoduše zahrnuje opakovanou diferenciaci funkce. Abychom tak mohli učinit, můžeme jednoduše aplikovat naše znalosti o pravidle moci. Uvažujme jako příklad funkci f (x) = x3 + 2×2-4x + 1. Pak:

první derivát: f'(x) = 3×2 + 4x-4

druhý derivát: f „(x) = 6x + 4

třetí derivát: f „‚ (x) = 6

čtvrtý derivát: f (4) (x) = 0

pátý derivát: f(5) (x) = 0 atd.

to, co jsme zde udělali, je to, že jsme nejprve použili pravidlo výkonu na f(x), abychom získali jeho první derivaci, f'(x), poté jsme použili pravidlo výkonu na první derivaci, abychom získali druhou a tak dále. Derivace se nakonec dostane na nulu, protože diferenciace je aplikována opakovaně.

použití pravidel produktu a kvocientu také zůstává platné při získávání derivátů vyššího řádu, ale jejich výpočet může být messier a messier, jak se objednávka zvyšuje. Obecné pravidlo Leibniz zjednodušuje úkol v tomto aspektu zobecněním pravidla produktu na:

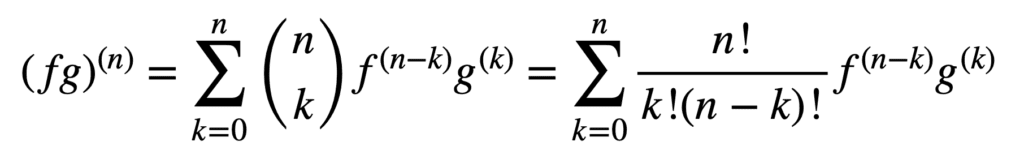
tady, termín, n! k!(n-k)!, je binomický koeficient z binomické věty, zatímco f (K) A g(k) označují KTH derivaci funkcí, F a g, resp.

proto nalezení první a druhé derivace (a tedy nahrazení n = 1 a n = 2) obecným leibnizovým pravidlem nám dává:

(fg) (1) = (fg) ‚= f (1) g + f g(1)

(fg) (2) = (fg) “ = f (2) g + 2f (1) g(1) + f g(2)

Všimněte si známého prvního derivátu definovaného pravidlem produktu. Leibnizovo pravidlo lze také použít k nalezení derivátů racionálních funkcí vyššího řádu, protože kvocient může být účinně vyjádřen do produktu formy, f g-1.

deriváty vícerozměrných funkcí vyššího řádu

definice parciálních derivátů vícerozměrných funkcí vyššího řádu je analogická s jednorozměrným případem: parciální derivace n-tého řádu pro n > 1 se vypočítá jako parciální derivace parciální derivace (n – 1). Například užívání druhého parciálního derivátu funkce se dvěma proměnnými má za následek čtyři, druhé parciální deriváty: dva vlastní parciální deriváty, fxx a fyy a dva zkřížené parciální deriváty, fxy a fyx.

abychom získali „derivaci“, musíme vzít parciální derivaci vzhledem k x nebo y a existují čtyři způsoby, jak to udělat: x pak x, x pak y, y pak x, y pak y.

– Strana 371, jednoduchý a vícerozměrný Počet, 2020.

uvažujme vícerozměrnou funkci, f (x, y) = x2 + 3xy + 4y2, pro kterou bychom chtěli najít druhé parciální derivace. Proces začíná nalezením jeho parciálních derivátů prvního řádu, nejprve: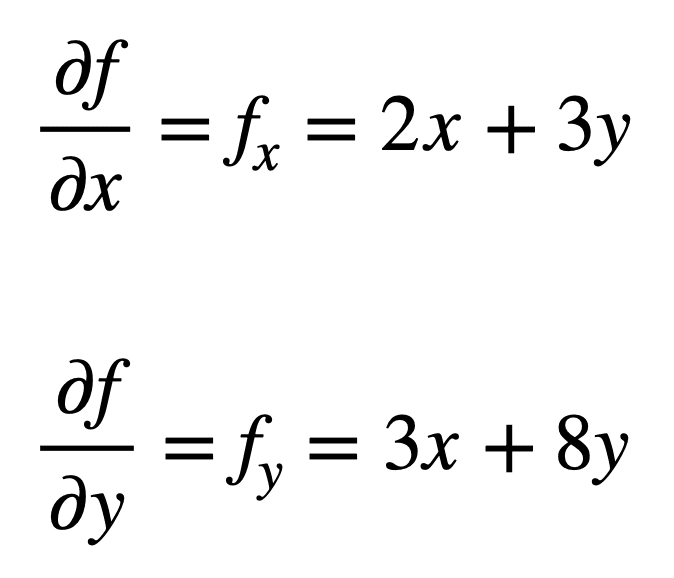

čtyři parciální deriváty druhého řádu se pak nacházejí opakováním procesu hledání parciálních derivátů parciálních derivátů. Vlastní parciální derivace jsou nejjednodušší k nalezení, protože jednoduše opakujeme proces částečné diferenciace, s ohledem na x nebo y, podruhé:

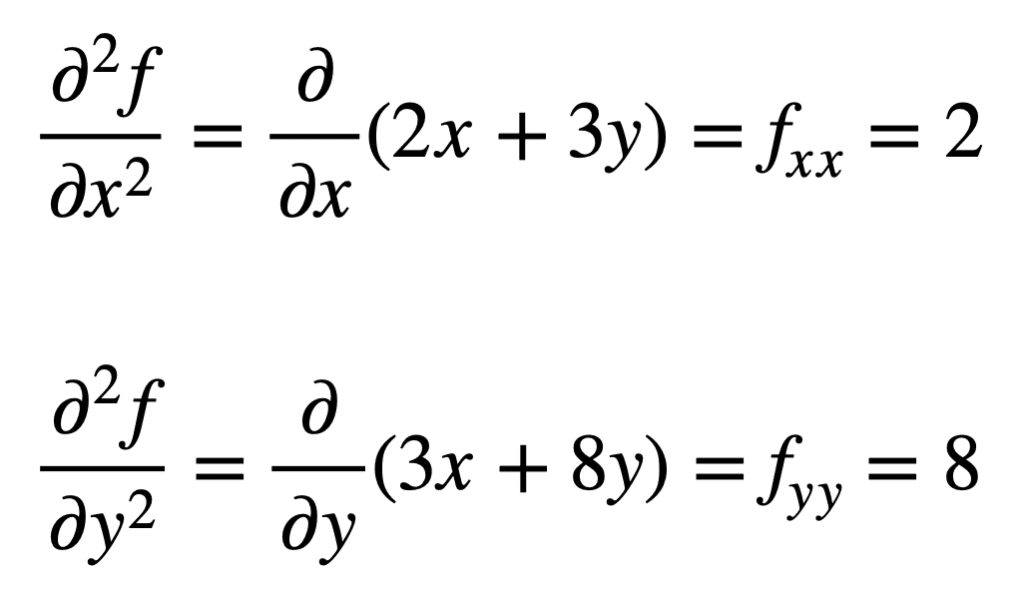
parciální derivát vzhledem k x) se nalézá tím, že se vezme parciální derivát výsledku vzhledem k y, což nám dává fxy. Podobně, vezmeme-li parciální derivaci fy vzhledem k x, dává nám fyx:

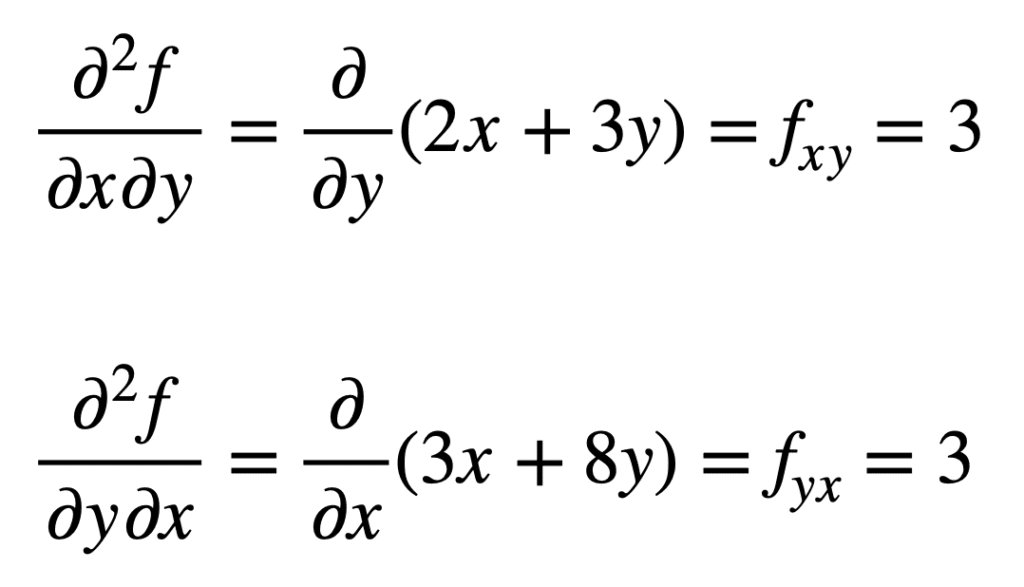
není náhodou, že křížové parciální deriváty dávají stejný výsledek. To je definováno Clairautovou větou, která uvádí, že pokud jsou křížové parciální derivace spojité, pak jsou stejné.

aplikace ve strojovém učení

ve strojovém učení se nejčastěji používá derivát druhého řádu. Již dříve jsme zmínili, že druhá derivace nám může poskytnout informace, které první derivace sama o sobě nemůže zachytit. Konkrétně nám může říci, zda je kritickým bodem lokální minimum nebo maximum (na základě toho, zda je druhá derivace větší nebo menší než nula), pro kterou by první derivace byla v obou případech nulová.

existuje několik optimalizačních algoritmů druhého řádu, které tyto informace využívají, jedním z nich je Newtonova metoda.

informace druhého řádu nám naproti tomu umožňují provést kvadratickou aproximaci objektivní funkce a přiblížit správnou velikost kroku k dosažení místního minima …

– Strana 87, algoritmy pro optimalizaci, 2019–

v jednorozměrném případě používá Newtonova metoda expanzi Taylorovy řady druhého řádu k provedení kvadratické aproximace kolem určitého bodu objektivní funkce. Pravidlo aktualizace pro Newtonovu metodu, které se získá nastavením derivátu na nulu a řešením pro kořen, zahrnuje operaci dělení druhou derivací. Pokud je Newtonova metoda rozšířena na vícerozměrnou optimalizaci, derivace je nahrazena gradientem, zatímco reciproční druhá derivace je nahrazena inverzí hesenské matice.

budeme pokrývat hesenské a Taylorovy řady aproximace, které využívají použití derivátů vyššího řádu, v samostatných tutoriálech.

další čtení

tato část poskytuje více zdrojů k tématu, pokud chcete jít hlouběji.

knihy

• Single a Multivariable Calculus, 2020.
• kalkul pro figuríny, 2016.
• Hluboké Učení, 2017.
• algoritmy pro optimalizaci, 2019.

shrnutí

v tomto tutoriálu jste zjistili, jak vypočítat univariační a vícerozměrné deriváty vyššího řádu.

konkrétně jste se naučili:

• Jak vypočítat deriváty vyššího řádu jednorozměrných funkcí.
• jak vypočítat deriváty vyššího řádu vícerozměrných funkcí.
• jak lze deriváty druhého řádu využít ve strojovém učení pomocí optimalizačních algoritmů druhého řádu.