Vad är t-testet med ett prov?
t-testet med ett prov är medlem i t-testfamiljen. Alla tester i t-testfamiljen jämför skillnader i medelvärden för kontinuerlig nivå (intervall eller Förhållande), normalt distribuerade data. Till skillnad från oberoende eller beroende prov T-test, fungerar ett prov T-test med endast ett medelvärde. T-testet med ett prov jämför medelvärdet för ett enda prov med ett förutbestämt värde för att bestämma om provets medelvärde är signifikant större eller mindre än det värdet.
det oberoende provet t-test jämför medelvärdet av en distinkt grupp med medelvärdet av en annan grupp. Ett exempel på forskningsfråga för ett oberoende prov T-test skulle vara, ” skiljer sig pojkar och flickor i sina SAT-poäng?”Det beroende provet t-testet jämför två matchade poäng eller mätningar (som före vs. efter). Ett exempel på forskningsfråga för ett beroende prov T-test skulle vara, ” förbättras elevernas betyg efter att de fått handledning?”
å andra sidan jämför t-testet med ett prov medelvärdet som finns i ett observerat prov till något förutbestämt eller hypotetiskt värde. Typiskt är det hypotetiska värdet populationsmedlet eller något annat teoretiskt härlett värde.

Upptäck hur vi hjälper till att redigera dina Avhandlingskapitel
anpassa teoretiska ramar, samla artiklar, syntetisera luckor, formulera en tydlig metodik och dataplan och skriva om de teoretiska och praktiska konsekvenserna av din forskning är en del av våra omfattande avhandlingstjänster.
- ta med avhandlingsredigeringsexpertis till kapitel 1-5 i tid.
- spåra alla ändringar och arbeta sedan med dig för att få till stånd vetenskapligt skrivande.
- pågående stöd för att ta itu med utskottets feedback, minska revideringar.
några möjliga tillämpningar av T-testet med ett prov inkluderar att testa ett prov mot ett förutbestämt eller förväntat värde, testa ett prov mot ett visst riktmärke eller testa resultaten från ett replikerat experiment mot den ursprungliga studien. Till exempel kan en forskare vilja avgöra om medelåldern för pensionering i en viss befolkning är 65. Forskaren skulle rita ett representativt urval av personer som går i pension och fråga vid vilken ålder de gick i pension. Ett T-test med ett prov kunde sedan utföras för att jämföra medelåldern som erhållits i provet (t.ex. 63) med det hypotetiska testvärdet på 65. T-testet avgör om skillnaden vi hittar i vårt prov är större än vi förväntar oss att se av en slump.
T-testet med ett prov i SPSS
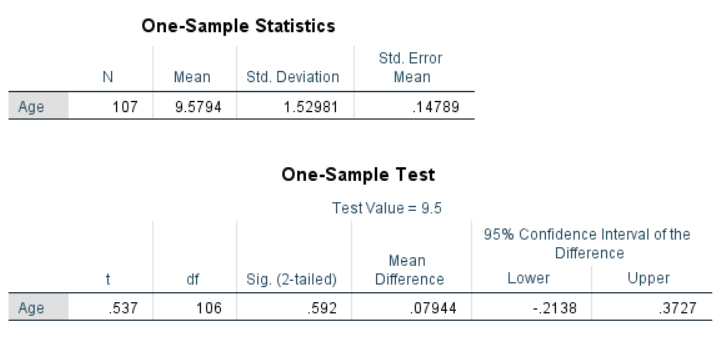
i det här exemplet kommer vi att genomföra ett T-test med ett prov för att avgöra om medelåldern för en befolkning av studenter är betydligt större eller mindre än 9,5 år.
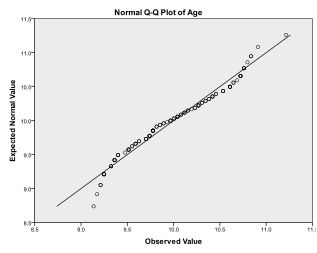
innan vi faktiskt genomför t-testet med ett prov är vårt första steg att kontrollera fördelningen för normalitet. Detta kan göras med en Q-Q-Plot (ligger under analysera > beskrivande statistik i SPSS). Sedan lägger vi helt enkelt till variabeln vi vill testa (ålder) i rutan och bekräftar att testfördelningen är inställd på Normal. Detta skapar diagrammet du ser nedan. Utgången visar att små värden och stora värden avviker något från normalitet. Som en extra kontroll kan vi köra ett Kolmogorov-Smirnov (K-S) – test för att testa nollhypotesen att variabeln normalt distribueras. Vi finner här att K-s-testet inte är signifikant; således kan vi inte avvisa nollhypotesen och kan anta att ålder är normalt fördelad.

Låt oss gå vidare till ett-prov T-test, som finns i Analysera > jämför betyder > ett-prov T-Test…
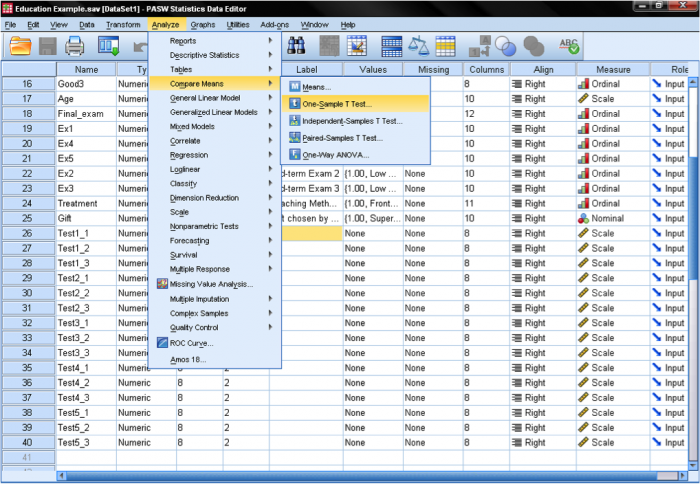
dialogrutan med ett prov T-test är ganska enkel. Vi lägger till testvariabeln ålder i listan över Testvariabler och anger sedan testvärdet. I vårt fall är det hypotetiska testvärdet 9,5. Dialogalternativen … ger oss inställningen för hur man hanterar saknade värden och även möjligheten att ange bredden på det konfidensintervall som används för testning.
när alla lämpliga alternativ är inställda klickar du på OK för att köra analysen. Figuren nedan visar utgången. Avsnittet ”Statistik med ett prov” visar beskrivande statistik för provet, inklusive medelvärdet som jämförs med testvärdet. Avsnittet ”ett provtest” visar resultaten från t-testet. I detta fall är nollhypotesen att medelvärdet av provet är lika med 9,5. För syftet med detta exempel kommer vi att ställa in vår betydelse (alfa) nivå till .05. Sig. kolumnen visar p-värdet för testet. Resultaten visar att p-värdet (.592) är större än .05. Detta tyder på att nollhypotesen inte kan avvisas, och provets ålder skiljer sig inte signifikant från 9.5.