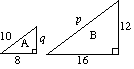en utvidgning är en transformation där ett objekt kartor till en bild av samma form men olika storlek. Objektet och bilden sägs vara liknande. En utvidgning kräver ett centrum för utvidgningen och en skalfaktor.
Notation
E är en utvidgning, med Centrum för utvidgningen O och skalfaktor 20.
E: AB 
AB
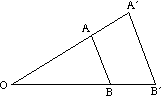
egenskaper för utvidgningen
triangel PQR kartor till triangel PQR under utvidgningen med centrum O.
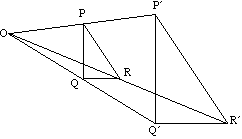
linjer och deras bilder är alltid parallella.
t.ex. PQ är parallell med PQ
Vinkelstorleken är invariant.
t.ex.
PQR =
utvidgningens centrum är den enda invarianta punkten.
längd och yta är inte oföränderliga, utom när m = 1 eller − 1.
dvs utvidgningen är inte en isometri.
utvidgningen är en direkt omvandling.
dvs
PQR och
om exporten är skalfaktorn för Längd, m 2 är skalfaktorn för Arean.
olika skalfaktorer
diagrammet nedan visar effekten av olika skalfaktorer på utvidgningen av en triangel ABC om centrum O.
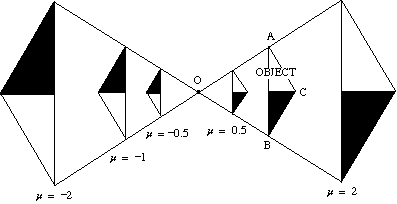
- om skalfaktorn är positiv är både objektet och bilden på samma sida av mitten.
- om skalfaktorn är negativ, är objektet och bilden på motsatta sidor av mitten.
bilden är inverterad.
se exempel på utvidgningar− 
placering av Centrum för utvidgningen
givet en figur och dess bild, för att hitta Centrum för utvidgningen:
1. Gå upp en punkt och dess image.
2. Upprepa för en annan punkt och dess bild.
3. Utvidgningens centrum är skärningspunkten mellan dessa linjer.
liknande siffror
siffrorna är likartade om de har samma form.
- liknande siffror kan kartläggas på varandra genom en utvidgning eller genom en kombination av reflektion, rotation eller översättning och en utvidgning.
- motsvarande vinklar av liknande siffror är lika.
- motsvarande sidor är proportionella mot varandra.
typ 1
YXZ liknar PQM eftersom de har motsvarande vinklar lika.
|
|
 |
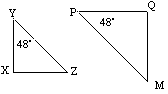YXZ kan mappas till PQM genom en kombination av transformationer.
Skalfaktor = = 
typ 2
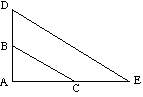
ABC liknar ADE eftersom:
|
(DE är parallellt med BC) |
 |
ABC kan mappas på ADE genom en utvidgning.
Skalfaktor = = 
|
(a) (i) de två trianglarna A och B är likartade. Hitta p och q. |
(a) (i) för A p = 2 × 10 p = 20 2 x q = 12 q = 6 |
|
(ii) området för triangel A är 24 enheter2. |
(ii) skalfaktor för area = 2 = 4 område av triangel B = 4 x område av triangel a |
|
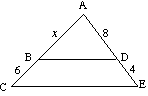
(B) Hitta x, om BD är parallell med CE |
(b) för
  12x = 8 (x + 6) 12x = 8x + 48 4x = 48 x = 12 |
B , skalfaktor = 2
ABD
ladda ner ett interaktivt kalkylblad (Microsoft Excel) som visar reflektioner, rotationer, översättningar och utvidgningar.
(Windows-användare, högerklicka och ” spara mål som…”för att spara filerna på din dator.)
