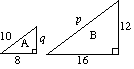uma ampliação é uma transformação em que um objeto mapeia para uma imagem da mesma forma, mas de tamanho diferente. O objeto e a imagem são considerados semelhantes. Um alargamento requer um centro de alargamento e um factor de escala.
Notação
E é um alargamento, com centro de alargamento e O fator de escala de µ.
E: AB 
AB
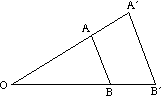
Propriedades do Alargamento
Triângulo PQR mapas para o triângulo PQR sob o alargamento com centro O.
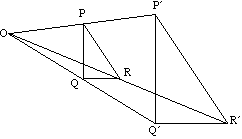
as linhas e suas imagens são sempre paralelas.
por exemplo, PQ é paralelo a pq
o tamanho do ângulo é invariante.
por exemplo
PQR =
o centro da ampliação é o único ponto invariante.
comprimento e área não são invariantes, exceto quando m = 1 ou − 1.
ou seja, o alargamento não é uma isometria.
o alargamento é uma transformação directa.
ou seja,
PQR e
Se μ for o Fator de escala para comprimento, mµ 2 é o Fator de escala para área.
Diferentes Fatores de Escala
O diagrama abaixo mostra o efeito de uma variedade de fatores de escala no alargamento de um triângulo ABC sobre o centro O.
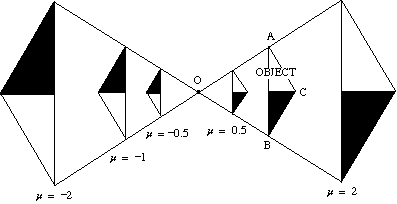
- Se o fator de escala é positivo, o objeto e a imagem estão no mesmo lado do centro.
- se o Fator de escala for negativo, o objeto e a imagem estão em lados opostos do centro.
a imagem é invertida.
Veja os exemplos de alargamentos− 
Localização do Centro de Alargamento
Dada uma figura e a sua imagem, para encontrar o centro de alargamento:
1. Junte-se a um ponto e sua imagem.
2. Repita para outro ponto e sua imagem.
3. O centro do alargamento é a intersecção destas linhas.
figuras semelhantes
figuras são semelhantes se tiverem a mesma forma.
- figuras semelhantes podem ser mapeadas umas sobre as outras por um alargamento ou por uma combinação de reflexão, rotação ou tradução e um alargamento.
- os ângulos correspondentes de figuras semelhantes são iguais.
- os lados correspondentes são proporcionais entre si.
tipo 1
YXZ é semelhante a PQM, pois eles têm ângulos correspondentes iguais.
|
|
 |
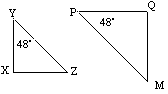YXZ pode ser mapeado para PQM por uma combinação de transformações.
fator de Escala = µ = 
Tipo 2
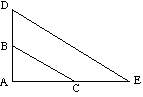
ABC é semelhante a ADE porque:
|
(DE é paralelo a BC) |
 |
ABC pode ser mapeada em ADE por uma ampliação.
fator de Escala = µ = 
|
(a) (i) Os dois triângulos A e B são semelhantes. Encontre p e Q. |
(a) (i) Para Um p = 2 × 10 p = 20 2 x q = 12 q = 6 |
|
(ii) A área de Um triângulo é de 24 units2. |
(ii) fator de Escala para a area = ķ2 = 4 Área do triângulo B = 4 x área do triângulo é Um |
|
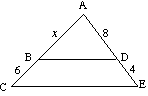
(b) Encontre x, se o BD é paralela a CE |
(b) Para
  12x = 8(x + 6) 12x = 8x + 48 4x = 48 x = 12 |
B , fator de escala = 2
ABD
Download interativo de folha de cálculo (Microsoft Excel), mostrando reflexões, rotações, translações e ampliações.
(usuários do Windows, clique com o botão direito e “Salvar destino como…”para salvar os arquivos no seu computador.)
