co to jest One-Sample t-Test?
test T z jedną próbką należy do rodziny testów T. We wszystkich testach z rodziny t-test porównuje się różnice w średniej punktacji wyników na poziomie ciągłym (interwał lub stosunek), danych o normalnym rozkładzie. W przeciwieństwie do niezależnych lub zależnych testów t, Test T z jedną próbką działa tylko z jednym średnim wynikiem. Test T z jedną próbką porównuje średnią z pojedynczej próbki z wcześniej określoną wartością, aby określić, czy średnia z próby jest znacznie większa lub mniejsza od tej wartości.
test t niezależnej próbki porównuje średnią jednej odrębnej grupy ze średnią innej grupy. Przykładowe pytanie badawcze dotyczące niezależnego testu t próbki brzmiałoby: „czy chłopcy i dziewczęta różnią się wynikami SAT?”Zależna próbka t-test porównuje dwa dopasowane wyniki lub pomiary (takie jak przed vs.po). Przykładowym pytaniem badawczym dla zależnej próbki t-testu byłoby: „czy oceny uczniów poprawiają się po otrzymaniu korepetycji?”
z drugiej strony, test T z jedną próbką porównuje średnią wynik znalezioną w obserwowanej próbce z pewną z góry określoną lub hipotetyczną wartością. Zazwyczaj hipotetyczną wartością jest średnia populacji lub inna teoretycznie pochodna wartość.

dowiedz się, jak pomagamy edytować rozdziały dysertacji
wyrównywanie ram teoretycznych, zbieranie artykułów, syntetyzowanie luk, formułowanie jasnej metodologii i planu danych oraz pisanie o teoretycznych i praktycznych implikacjach badań są częścią naszych kompleksowych usług edycji dysertacji.
- doprowadzić rozprawa editing expertise do rozdziałów 1-5 w odpowiednim czasie.
- Śledź wszystkie zmiany, a następnie współpracuj z Tobą, aby doprowadzić do pisania naukowego.
- bieżące wsparcie w zakresie rozpatrywania opinii Komitetu, zmniejszanie zmian.
niektóre możliwe zastosowania testu T z jedną próbką obejmują testowanie próbki w stosunku do z góry określonej lub oczekiwanej wartości, testowanie próbki w stosunku do określonego punktu odniesienia lub testowanie wyników replikowanego eksperymentu w stosunku do pierwotnego badania. Na przykład badacz może chcieć ustalić, czy średni wiek przechodzenia na emeryturę w określonej populacji wynosi 65 lat. Badacz narysuje reprezentatywną próbkę osób wchodzących na emeryturę i zapyta, w jakim wieku przeszli na emeryturę. Następnie można przeprowadzić test T z jedną próbką w celu porównania średniej wieku uzyskanej w próbce (np. 63) Z hipotetyczną wartością testu wynoszącą 65. Test t określa, czy różnica, którą znajdujemy w naszej próbce, jest większa niż spodziewalibyśmy się zobaczyć przez przypadek.
Test T z jedną próbką w SPSS
w tym przykładzie przeprowadzimy test T z jedną próbką, aby określić, czy średni wiek populacji studentów jest znacznie większy lub mniejszy niż 9,5 roku.
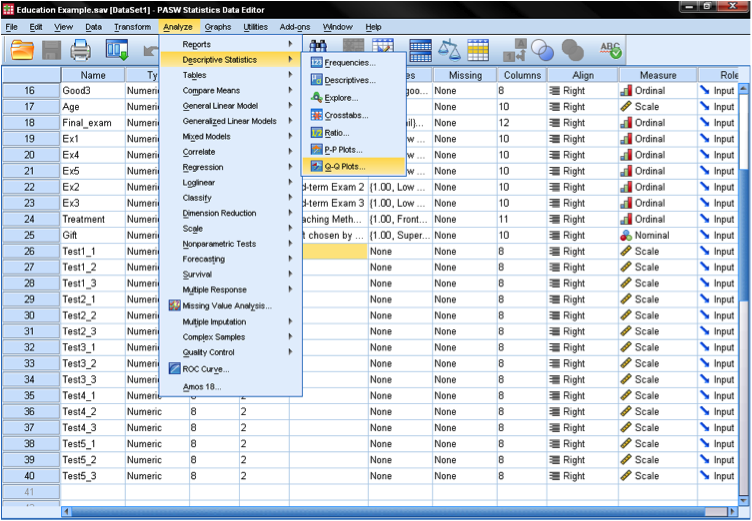
zanim faktycznie przeprowadzimy test T z jedną próbką, naszym pierwszym krokiem jest sprawdzenie rozkładu pod kątem normalności. Można to zrobić za pomocą wykresu Q-Q (znajdującego się pod Analizuj > statystyki opisowe w SPSS). Następnie po prostu dodajemy do pola zmienną, którą chcemy przetestować (wiek) i potwierdzamy, że rozkład testowy jest ustawiony na normalny. Spowoduje to utworzenie diagramu, który widzisz poniżej. Wynik pokazuje, że małe wartości i duże wartości nieco odbiegają od normalności. Jako dodatkowe sprawdzenie, możemy uruchomić Kołmogorov-Smirnov (K-S) test, aby przetestować hipotezę zerową, że zmienna jest normalnie rozłożone. Znajdujemy tutaj, że test K-S nie jest znaczący; dlatego nie możemy odrzucić hipotezy zerowej i możemy założyć, że wiek jest normalnie rozłożony.

przejdźmy do testu T z jedną próbką, który można znaleźć w Analizuj > Porównaj oznacza > Test T z jedną próbką…
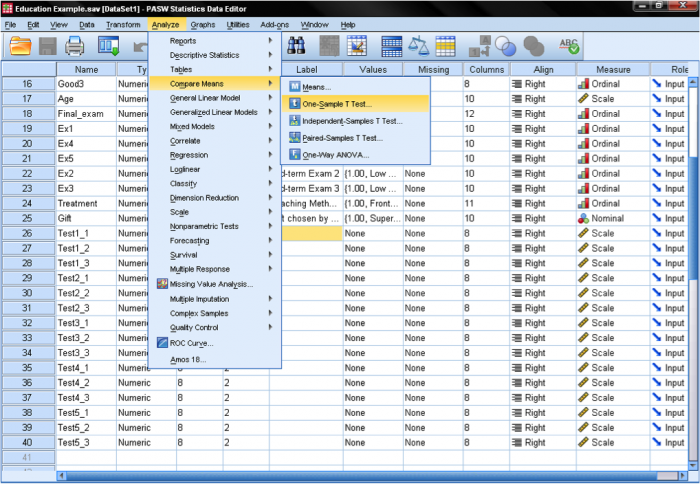
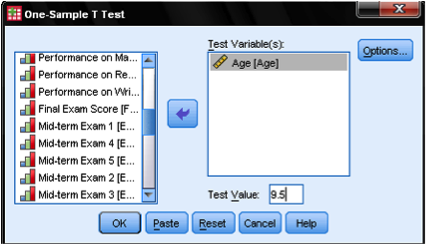
okno dialogowe one-sample t-test jest dość proste. Do listy zmiennych testowych dodajemy zmienną test age, a następnie wprowadzamy wartość testową. W naszym przypadku hipotetyczna wartość testu wynosi 9,5. Okno dialogowe Opcje … daje nam ustawienie zarządzania brakujących wartości, a także możliwość określenia szerokości przedziału ufności używanego do testowania.
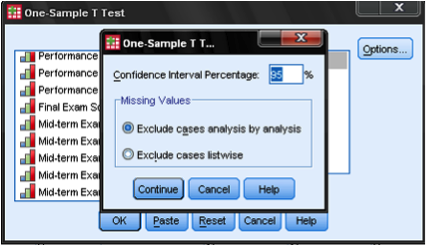
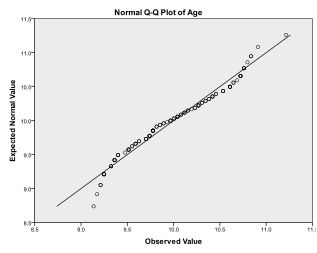
po ustawieniu wszystkich odpowiednich opcji kliknij OK, aby uruchomić analizę. Poniższy rysunek pokazuje dane wyjściowe. Sekcja „statystyki dotyczące jednej próbki” pokazuje statystyki opisowe dla próbki, w tym średnią porównywaną z wartością badania. Sekcja „Test na jedną próbkę”pokazuje wyniki testu T. W tym przypadku hipoteza zerowa jest taka, że średnia próbki jest równa 9,5. Na potrzeby tego przykładu ustawimy nasz poziom istotności (alfa) na.05. Sig. w kolumnie wyświetlana jest wartość p dla badania. Wyniki pokazują, że wartość p (.592) jest większa od05. Sugeruje to, że hipotezy zerowej nie można odrzucić, a wiek próbki nie różni się znacząco od 9.5.