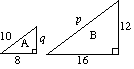powiększenie to przekształcenie, w którym obiekt mapuje obraz o tym samym kształcie, ale o innym rozmiarze. Mówi się, że obiekt i obraz są podobne. Rozszerzenie wymaga centrum rozszerzenia i czynnika skali.
notacja
E jest rozszerzeniem o środku rozszerzenia O i współczynniku skali µ.
E: AB 
AB
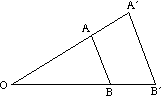
właściwości powiększenia
Trójkąt PQR mapuje do trójkąta PQR pod powiększeniem o Centrum O.
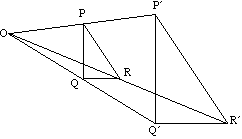
linie i ich obrazy są zawsze równoległe.
np. PQ jest równoległe do PQ
Rozmiar kąta jest niezmienny.
np.
PQR =
środek rozszerzenia jest jedynym punktem niezmienniczym.
długość i powierzchnia nie są niezmienne, z wyjątkiem sytuacji, gdy m = 1 lub − 1.
tzn. powiększenie nie jest izometrią.
rozszerzenie jest przekształceniem bezpośrednim.
tj.
PQR i
jeśli μ jest współczynnikiem skali dla długości, mµ 2 jest współczynnikiem skali dla powierzchni.
różne współczynniki skali
poniższy diagram pokazuje wpływ różnych współczynników skali na powiększenie trójkąta ABC o środku O.
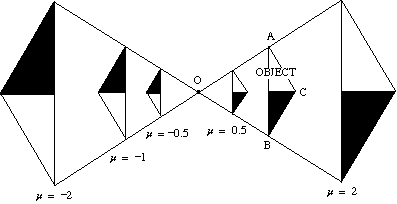
- jeśli współczynnik skali jest dodatni, zarówno obiekt, jak i obraz znajdują się po tej samej stronie środka.
- jeśli współczynnik skali jest ujemny, obiekt i obraz znajdują się po przeciwnych stronach środka.
obraz jest odwrócony.
zobacz przykłady powiększeń− 
położenie środka rozszerzenia
aby znaleźć środek rozszerzenia, Należy podać rysunek i jego obraz:
1. Połącz punkt i jego wizerunek.
2. Powtórz dla innego punktu i jego obrazu.
3. Środkiem rozszerzenia jest przecięcie tych linii.
podobne figury
figury są podobne, jeśli mają ten sam kształt.
- podobne liczby można odwzorować na siebie przez powiększenie lub połączenie odbicia, obrotu lub tłumaczenia i rozszerzenia.
- odpowiednie kąty podobnych figur są równe.
- odpowiednie boki są proporcjonalne do siebie.
Typ 1
YXZ jest podobny do PQM, ponieważ mają odpowiednie kąty równe.
|
|
 |
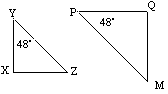YXZ można odwzorować na PQM przez kombinację przekształceń.
współczynnik skali = µ = 
Typ 2
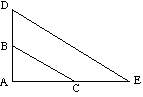
ABC jest podobne do ADE, ponieważ:
|
(DE jest równoległe do BC) |
 |
ABC można odwzorować na ADE przez powiększenie.
współczynnik skali = µ = 
|
(a) (i) dwa trójkąty a i B są podobne. Znajdź p i Q. |
(a) (i) dla a p = 2 × 10 p = 20 2 x q = 12 q = 6 |
|
(ii) powierzchnia trójkąta a wynosi 24 jednostki2. |
(ii) współczynnik skali dla obszaru = µ2 = 4 obszaru trójkąta B = 4 x obszaru trójkąta a |
|
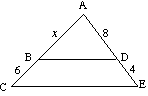
(b) Znajdź x, jeśli BD jest równoległa do CE |
(b) Dla
  12x = 8 (x + 6) 12x = 8x + 48 4x = 48 x = 12 |
B, współczynnik skali = 2
ABD
Pobierz interaktywny arkusz kalkulacyjny (Microsoft Excel) pokazujący refleksje, obroty, tłumaczenia i powiększenia.
(użytkowników systemu Windows, kliknij prawym przyciskiem myszy i ” Zapisz cel jako…”aby zapisać pliki na komputerze.)
