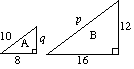en utvidelse er en transformasjon der et objekt kartlegger til et bilde av samme form, men forskjellig størrelse. Objektet og bildet sies å være like. En utvidelse krever et senter for utvidelse og en skala faktor.
Notasjon
E er en utvidelse, med senter for utvidelse O Og skala faktor µ.
E: AB 
AB
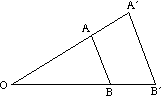
Egenskaper For Utvidelse
Trekant Pqr kart til trekant PQR under utvidelse med sentrum O.
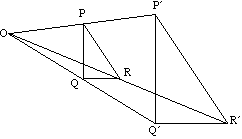
Linjer og deres bilder er alltid parallelle.
F. eks. ER pq parallell med PQ
Vinkelstørrelsen er invariant.
f. eks.
PQR =
sentrum av utvidelsen er det eneste invariante punktet.
Lengde og areal er ikke invariant, unntatt når m = 1 eller-1.
Dvs.Utvidelse er ikke en isometri.
Utvidelse er en direkte transformasjon.
dvs.
PQR og
hvis μ er skalafaktoren for lengde, er mµ 2 skalafaktoren for areal.
Ulike Skalafaktorer
diagrammet nedenfor viser effekten av en rekke skalafaktorer på utvidelsen av en trekant ABC om sentrum o.
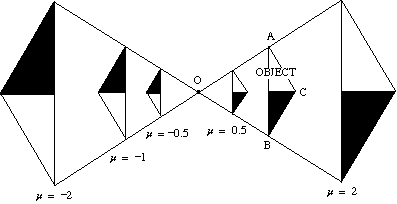
- hvis skalafaktoren er positiv, er både objektet og bildet på samme side av senteret.
- hvis skalafaktoren er negativ, er objektet og bildet på motsatte sider av midten.
bildet er invertert.
Se eksempler på forstørrelser− 
Plassering Av Sentrum Av Utvidelsen
Gitt en figur og dens bilde, for å finne sentrum av utvidelsen:
1. Bli med opp et punkt og dets bilde.
2. Gjenta for et annet punkt og dets bilde.
3. Senter for utvidelse er skjæringspunktet mellom disse linjene.
Lignende Figurer
Figurer er like hvis de har samme form.
- Lignende figurer kan kartlegges på hverandre ved en utvidelse eller ved en kombinasjon av refleksjon, rotasjon eller oversettelse og en utvidelse.
- de tilsvarende vinklene til lignende figurer er like.
- de tilsvarende sidene er proporsjonale med hverandre.
Type 1
YXZ ligner PQM da de har tilsvarende vinkler like.
|
|
 |
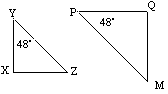YXZ kan kartlegges til PQM ved en kombinasjon av transformasjoner.
Skalafaktor = µ = 
Type 2
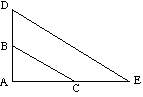
ABC ligner ade fordi:
|
(DE er parallell MED BC) |
 |
ABC kan kartlegges på ADE ved en utvidelse.
Skalafaktor = µ = 
|
(a) (i) de to trekantene A Og B er like. Finn p og q. |
(a) (i) For A p = 2 × 10 p = 20 2 x q = 12 q = 6 |
|
(ii) arealet av trekant A er 24 enheter2. |
(ii) Skalafaktor for areal = µ2 = 4 område av trekant b = 4 x område av trekant A |
|
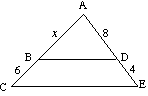
(B) Finn x, HVIS BD er parallell MED CE |
(b) for
  12x = 8 (x + 6) 12x = 8x + 48 4x = 48 x = 12 |
B, skala faktor = 2 
ABD
Last ned et interaktivt regneark (Microsoft Excel) som viser refleksjoner, rotasjoner, oversettelser og forstørrelser.
(Windows-brukere, høyreklikk og » Lagre mål som…»for å lagre filene på datamaskinen din.)
