mikä on yhden näytteen T-testi?
yhden näytteen t-testi kuuluu t-testiperheeseen. Kaikissa t-testiperheeseen kuuluvissa testeissä verrataan yleensä jaettujen tulosten eroja jatkuvan tason keskiarvoissa (intervalli tai suhde). Toisin kuin riippumattomat tai riippuvaiset t-testit, yhden näytteen t-testi toimii vain yhdellä pistekeskiarvolla. Yhden näytteen t-testissä verrataan yksittäisen näytteen keskiarvoa ennalta määrättyyn arvoon sen määrittämiseksi, onko näytteen keskiarvo merkittävästi suurempi vai pienempi kuin kyseinen arvo.
riippumattomassa t-näytteessä verrataan yhden erillisen ryhmän keskiarvoa toisen ryhmän keskiarvoon. Esimerkki tutkimus kysymys riippumaton näyte t-testi olisi, ” ovatko pojat ja tytöt eroavat niiden SAT tulokset?”Riippuvainen näyte t-testi vertaa kahta täsmäävää pistemäärää tai mittausta (kuten ennen vs. jälkeen). Esimerkki tutkimuskysymys riippuvaiselle t-testille olisi: ”Paranevatko oppilaiden arvosanat sen jälkeen, kun he saavat tutorointia?”
toisaalta yhden näytteen t-testi vertaa havaitun näytteen keskiarvoa johonkin ennalta määrättyyn tai hypoteettiseen arvoon. Tyypillisesti hypoteettinen arvo on populaation keskiarvo tai jokin muu teoreettisesti johdettu arvo.

tutustu siihen, miten avustamme Väitöskirjasi lukujen muokkaamisessa
teoreettisen viitekehyksen yhtenäistämisessä, artikkelien keräämisessä, aukkojen tiivistämisessä, selkeän metodologian ja datasuunnitelman artikuloimisessa sekä tutkimustesi teoreettisista ja käytännön vaikutuksista kirjoittamisessa ovat osa kattavia väitöskirjan editointipalvelujamme.
- tuo väitöskirjan editointiosaaminen lukuihin 1-5 ajoissa.
- seuraa kaikki muutokset ja työskentele sitten kanssasi tieteellisen kirjoittamisen aikaansaamiseksi.
- jatkuva tuki komiteapalautteen käsittelylle, mikä vähentää tarkistuksia.
yhden näytteen t-testin joitakin mahdollisia sovelluksia ovat näytteen testaaminen ennalta määrättyyn tai odotettuun arvoon, näytteen testaaminen tiettyyn vertailuarvoon tai toistetun kokeen tulosten testaaminen alkuperäiseen tutkimukseen. Tutkija voi esimerkiksi haluta selvittää, onko tietyn väestön eläkkeelle jäämisen keski-ikä 65 vuotta. Tutkija vetäisi edustavan otoksen eläkkeelle siirtyvistä ihmisistä ja kysyisi, missä iässä he ovat jääneet eläkkeelle. Tämän jälkeen voidaan tehdä yhden näytteen t-testi, jossa vertaillaan otoksesta saatua keski-ikää (esim.63) hypoteettiseen testiarvoon 65. T-testi määrittää, onko otoksestamme löytämämme ero suurempi kuin mitä odottaisimme sattumalta näkevämme.
yhden otoksen T-testi SPSS: ssä
tässä esimerkissä teemme yhden otoksen t-testin selvittääksemme, onko opiskelijaväestön keski-ikä merkittävästi suurempi vai alle 9,5 vuotta.
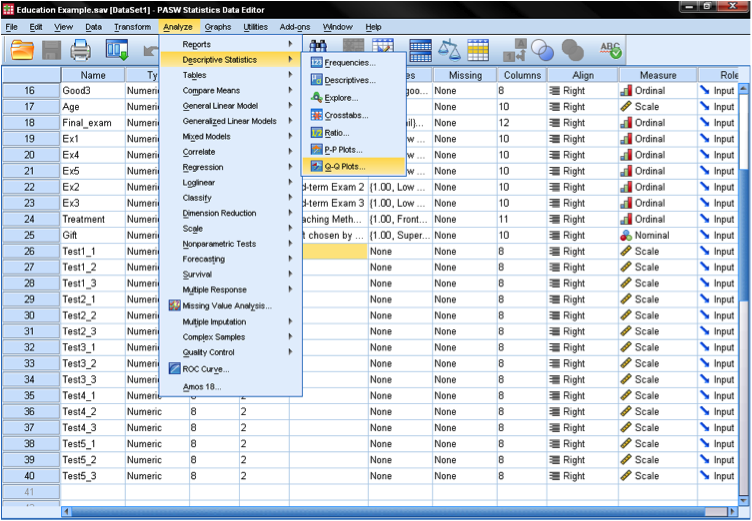
ennen kuin todella suoritamme yhden näytteen t-testi, meidän ensimmäinen askel on tarkistaa Jakelu normaalius. Tämä voidaan tehdä Q-Q-Kuvaajalla (sijaitsee analysoitaessa > kuvailevia tilastoja SPSS: ssä). Sitten lisäämme ruutuun testattavan muuttujan (ikä) ja vahvistamme, että testijakauma on normaali. Tämä luo alla olevan kaavion. Lähtö osoittaa, että pienet ja suuret arvot poikkeavat jonkin verran normaaliudesta. Lisätarkistuksena voidaan suorittaa Kolmogorov-Smirnov (K-S) – testi, jolla testataan nollahypoteesia, jonka mukaan muuttuja on normaalisti jakautunut. Huomaamme tässä, että K-s-testi ei ole merkittävä, joten emme voi hylätä nollahypoteesia ja voimme olettaa, että ikä on normaalisti jakautunut.

siirrytään yhden näytteen t-testiin, joka löytyy analyysistä > vertaa keskiarvoja > yhden näytteen T-testi…
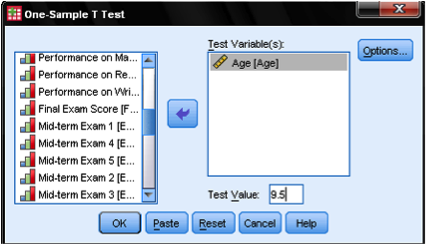
yhden näytteen t-testi-valintaikkuna on melko yksinkertainen. Lisätään testimuuttujan Ikä Testimuuttujien luetteloon ja syötetään sitten testiarvo. Meidän tapauksessamme hypoteettinen testiarvo on 9,5. Valintaikkuna-Asetukset … antaa meille asetuksen puuttuvien arvojen hallintaan ja mahdollisuuden määrittää testauksessa käytetyn luottamusvälin leveys.
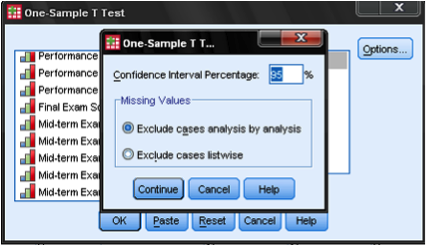
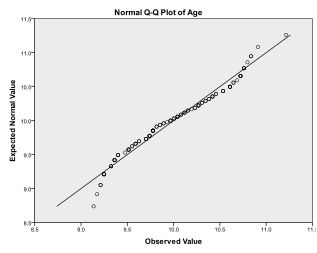
kun kaikki sopivat vaihtoehdot on asetettu, suorita analyysi napsauttamalla OK. Alla oleva kuva näyttää tuotoksen. ”Yhden otoksen tilastot” -osiossa esitetään otoksen kuvaavia tilastoja, mukaan lukien keskiarvo, jota verrataan testiarvoon. ”Yhden näytteen testi” -osiossa esitetään t-testin tulokset. Tällöin nollahypoteesin mukaan otoksen keskiarvo on 9,5. Tätä esimerkkiä varten asetamme merkityksemme (alfa) tasolle .05. Sig. sarake näyttää testin p-arvon. Tulokset osoittavat, että p-arvo (.592) on suurempi kuin .05. Tämä viittaa siihen, että nollahypoteesia ei voida hylätä, eikä otoksen Ikä poikkea merkittävästi 9: stä.5.