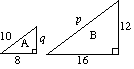en udvidelse er en transformation, hvor et objekt kortlægges til et billede af samme form, men forskellig størrelse. Objektet og billedet siges at være ens. En udvidelse kræver et centrum for udvidelsen og en skalafaktor.
Notation
E er en udvidelse, med centrum for udvidelsen O og skalafaktoren Hr.
E: AB 
AB
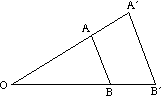
udvidelsens egenskaber
Trekantpkr kort til trekantpkr under udvidelse med Center O.
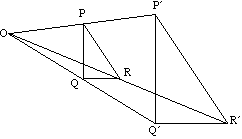
linjer og deres billeder er altid parallelle.
f.eks. er PK parallel med PK
vinkelstørrelsen er invariant.
f.eks.
PKR =
udvidelsens centrum er det eneste uforanderlige punkt.
længde og areal er ikke uforanderlige, undtagen når m = 1 eller − 1.
dvs.udvidelse er ikke en isometri.
udvidelse er en direkte transformation.
dvs.
PKR og
hvis kr.er skalafaktoren for længde, er kr. 2 skalafaktoren for areal.
forskellige Skalafaktorer
diagrammet nedenfor viser effekten af en række skalafaktorer på udvidelsen af en trekant ABC om Center O.
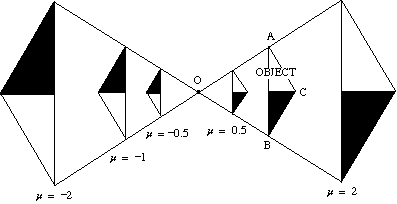
- hvis skalafaktoren er positiv, er både objektet og billedet på samme side af midten.
- hvis skalafaktoren er negativ, er objektet og billedet på modsatte sider af midten.
billedet er omvendt.
se eksempler på udvidelser− 
placering af centrum for udvidelsen
givet en figur og dens billede, for at finde centrum for udvidelsen:
1. Deltag i et punkt og dets Billede.
2. Gentag for et andet punkt og dets Billede.
3. Centrum for udvidelsen er skæringspunktet mellem disse linjer.
lignende tal
tal er ens, hvis de har samme form.
- lignende tal kan kortlægges på hinanden ved en udvidelse eller ved en kombination af refleksion, rotation eller oversættelse og en udvidelse.
- de tilsvarende vinkler af lignende figurer er ens.
- de tilsvarende sider er proportionale med hinanden.
Type 1
kvm, da de har tilsvarende vinkler ens.
|
|
 |
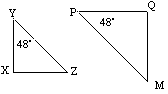kan kortlægges til kvm ved en kombination af transformationer.
skalafaktor = venstre = 
Type 2
ABC svarer til Ade fordi:
|
(de er parallel med BC) |
 |
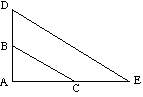ABC kan kortlægges på ADE ved en udvidelse.
skalafaktor = venstre = 
|
(A) (i) de to trekanter A og B er ens. Find p og K. |
(A) (i) for a p = 2 × 10 p = 20 2 gange K = 12 K = 6 |
|
(ii) arealet af trekant A er 24 enheder2. |
(ii) skalafaktor for areal = kr2 = 4 areal af trekant B = 4 gange areal af Trekant a |
|
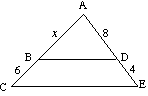
(B) Find h, hvis BD er parallel med CE |
(b) for
  12 gange = 8 (+6) 12 gange = 8 gange + 48 4 gange = 48 = 12 |
B , skalafaktor = 2
ABD
Hent et interaktivt regneark, der viser refleksioner, rotationer, oversættelser og udvidelser.
(vinduer brugere, højreklik og ” gem mål som…”for at gemme filerne på din computer.)
