co je jeden vzorek T-Test?
t-test s jedním vzorkem je členem rodiny t-testů. Všechny testy v rodině t-testů porovnávají rozdíly v průměrných skóre kontinuálních úrovní (interval nebo poměr), normálně distribuovaných dat. Na rozdíl od nezávislých nebo závislých t-testů pracuje t-test s jedním vzorkem pouze s jedním průměrným skóre. T-test s jedním vzorkem porovnává průměr jednoho vzorku s předem stanovenou hodnotou, aby se určilo, zda je průměr vzorku významně větší nebo menší než tato hodnota.
nezávislý t-test vzorku porovnává průměr jedné odlišné skupiny s průměrem jiné skupiny. Příkladem výzkumné otázky pro nezávislý vzorek t-testu by bylo, “ chlapci a dívky se liší v jejich skóre SAT.“?“Závislý vzorek t-test porovnává dvě shodná skóre nebo měření (například před vs. po). Příkladem výzkumné otázky pro závislý vzorek t-testu by bylo, “ zlepšují se známky žáků po doučování?“?“
na druhé straně t-test jednoho vzorku porovnává průměrné skóre nalezené v pozorovaném vzorku s určitou předem stanovenou nebo hypotetickou hodnotou. Hypotetickou hodnotou je obvykle průměr populace nebo nějaká jiná teoreticky odvozená hodnota.

Objevte, jak pomáháme upravovat kapitoly Disertační práce
sladění teoretického rámce, shromažďování článků, syntéza mezer, formulování jasné metodiky a datového plánu a psaní o teoretických a praktických důsledcích vašeho výzkumu jsou součástí našich komplexních služeb pro editaci disertačních prací.
- Přineste odbornost editace disertační práce do kapitol 1-5 včas.
- Sledujte všechny změny a poté s vámi spolupracujte na vědeckém psaní.
- pokračující podpora pro řešení zpětné vazby výboru, snížení revizí.
některé možné Aplikace t-testu s jedním vzorkem zahrnují testování vzorku proti předem stanovené nebo očekávané hodnotě, testování vzorku proti určitému benchmarku nebo testování výsledků replikovaného experimentu proti původní studii. Například výzkumník může chtít určit, zda je průměrný věk odchodu do důchodu v určité populaci 65 let. Výzkumník by nakreslil reprezentativní vzorek lidí vstupujících do důchodu a zeptal se, v jakém věku odešli do důchodu. T-test s jedním vzorkem by pak mohl být proveden za účelem porovnání průměrného věku získaného ve vzorku (např. 63) s hypotetickou zkušební hodnotou 65. T-test určuje, zda je rozdíl, který najdeme v našem vzorku, větší, než bychom očekávali náhodou.
T-Test s jedním vzorkem v SPSS
v tomto příkladu provedeme t-test s jedním vzorkem, abychom zjistili, zda je průměrný věk populace studentů výrazně větší nebo menší než 9,5 let.
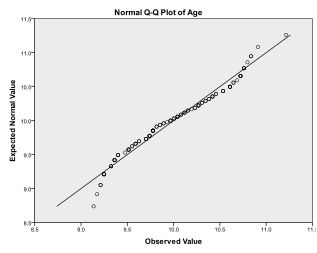
než skutečně provedeme t-test s jedním vzorkem, naším prvním krokem je zkontrolovat normálnost distribuce. To lze provést pomocí grafu Q-Q (umístěného v části analyzovat > popisné statistiky v SPSS). Poté jednoduše přidáme proměnnou, kterou chceme testovat (věk), do pole a potvrdíme, že distribuce testu je nastavena na normální. Tím se vytvoří diagram, který vidíte níže. Výstup ukazuje, že malé hodnoty a velké hodnoty se poněkud odchylují od normality. Jako další kontrolu můžeme spustit test Kolmogorov-Smirnov (K-S), abychom otestovali nulovou hypotézu, že proměnná je normálně distribuována. Zjistili jsme, že test K-S není významný; tím pádem, nemůžeme odmítnout nulovou hypotézu a můžeme předpokládat, že věk je normálně distribuován.

pojďme k t-testu s jedním vzorkem, který lze nalézt v analýze > porovnat prostředky > test s jedním vzorkem T…
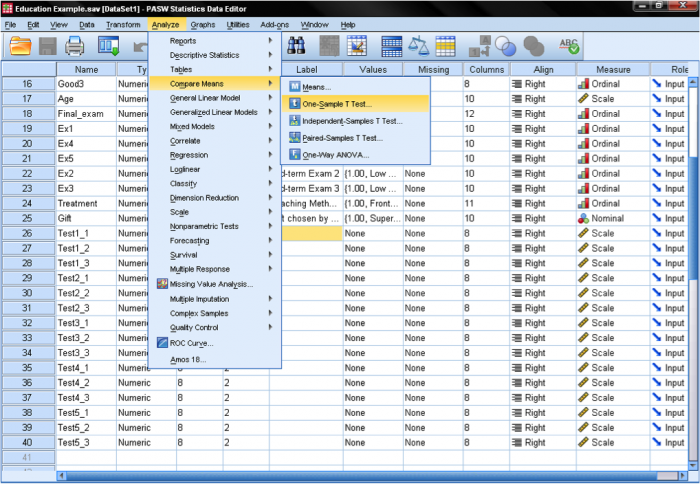
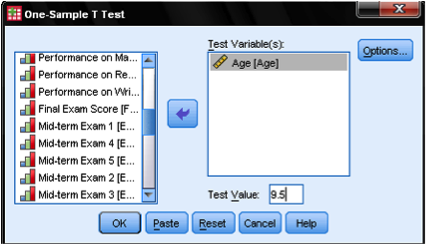
dialogové okno t-test s jedním vzorkem je poměrně jednoduché. Do seznamu testovaných proměnných přidáme testovací proměnnou age a poté zadáme testovací hodnotu. V našem případě je hypotetická hodnota testu 9,5. Možnosti dialogu … nám dávají nastavení pro správu chybějících hodnot a také možnost určit šířku intervalu spolehlivosti použitého pro testování.
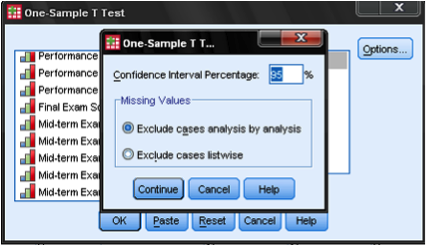
po nastavení všech příslušných možností spusťte analýzu kliknutím na OK. Níže uvedený obrázek ukazuje výstup. V části „Statistika jednoho vzorku“ jsou uvedeny popisné statistiky vzorku, včetně průměru porovnávaného se zkušební hodnotou. V části „Test jednoho vzorku“ jsou uvedeny výsledky t-testu. V tomto případě je nulová hypotéza, že průměr vzorku se rovná 9,5. Pro účely tohoto příkladu nastavíme naši úroveň významnosti (alfa) na .05. Sig. sloupec zobrazuje hodnotu p pro test. Výsledky ukazují, že hodnota p (.592) je větší než.05. To naznačuje, že nulovou hypotézu nelze odmítnout a věk vzorku se významně neliší od 9.5.