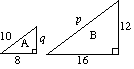Un agrandissement est une transformation dans laquelle un objet est mappé à une image de la même forme mais de taille différente. L’objet et l’image sont dits similaires. Un élargissement nécessite un centre d’élargissement et un facteur d’échelle.
La notation
E est un élargissement, avec le centre d’élargissement O et le facteur d’échelle µ.
E: AB 
AB
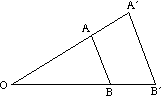
Propriétés de l’élargissement
Le triangle PQR correspond au triangle PQR sous élargissement avec le centre O.
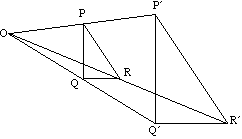
Les lignes et leurs images sont toujours parallèles.
par exemple PQ est parallèle à PQ
La taille de l’angle est invariante.
par exemple
PQR =
Le centre de l’élargissement est le seul point invariant.
La longueur et l’aire ne sont pas invariantes, sauf si m = 1 ou -1.
c’est-à-dire que l’agrandissement n’est pas une isométrie.
L’agrandissement est une transformation directe.
c’est-à-dire
PQR et
Si μ est le facteur d’échelle pour la longueur, mµ 2 est le facteur d’échelle pour la surface.
Différents facteurs d’échelle
Le diagramme ci-dessous montre l’effet d’une variété de facteurs d’échelle sur l’élargissement d’un triangle ABC autour du centre O.
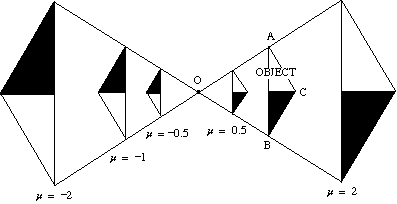
- Si le facteur d’échelle est positif, l’objet et l’image sont du même côté du centre.
- Si le facteur d’échelle est négatif, l’objet et l’image se trouvent sur les côtés opposés du centre.
L’image est inversée.
Voir des exemples d’agrandissements − 
Localisation du Centre d’agrandissement
Compte tenu d’une figure et de son image, pour trouver le centre d’agrandissement :
1. Joignez un point et son image.
2. Répétez pour un autre point et son image.
3. Le centre de l’élargissement est l’intersection de ces lignes.
Figures similaires
Les figures sont similaires si elles ont la même forme.
- Des figures similaires peuvent être cartographiées les unes sur les autres par un agrandissement ou par une combinaison de réflexion, de rotation ou de translation et d’un agrandissement.
- Les angles correspondants de figures similaires sont égaux.
- Les côtés correspondants sont proportionnels les uns aux autres.
Type 1
YXZ est similaire à PQM car ils ont des angles correspondants égaux.
|
|
 |
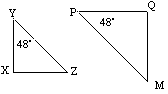YXZ peut être mappé à PQM par une combinaison de transformations.
Facteur d’échelle = µ = 
Type 2
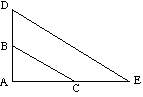
ABC est similaire à ADE car:
|
(DE est parallèle à BC) |
 |
ABC peut être mappé sur ADE par un agrandissement.
Facteur d’échelle = µ = 
|
( a) (i) Les deux triangles A et B sont similaires. Trouvez p et q. |
( a) (i) Pour A p = 2 × 10 p = 20 2 x q = 12 q = 6 |
|
( ii) L’aire du triangle A est de 24 unités2. |
( ii) Facteur d’échelle pour l’aire = µ2 = 4 Aire du triangle B = 4 x aire du triangle A |
|
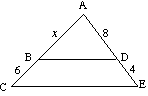
( b) Trouver x, si BD est parallèle à CE |
( b) Pour
  12x = 8 (x+6) 12x = 8x+48 4x = 48 x = 12 |
B, facteur d’échelle = 2 
ABD
Téléchargez une feuille de calcul interactive (Microsoft Excel) montrant les réflexions, les rotations, les traductions et les agrandissements.
( Utilisateurs Windows, faites un clic droit et « Enregistrer la cible sous… »pour enregistrer les fichiers sur votre ordinateur.)
